マルコフ性

マルコフ性（まるこふせい、（英: Markov property）は確率過程が持ちうる「現在状態が明らかなら、未来状態は過去履歴から独立して予測される」という性質である。

概要

マルコフ性は確率過程が持ちうる特性の一種で「過程の将来状態の条件付き確率分布が、現在状態のみに依存し、過去のいかなる状態にも依存しない」ことをいう（⇒ #定義）。すなわち、過去の状態が与えられたとき、現在の状態（過程の経路）は条件付き独立である。

この性質はロシア人数学者のアンドレイ・マルコフにちなんで名付けられた。

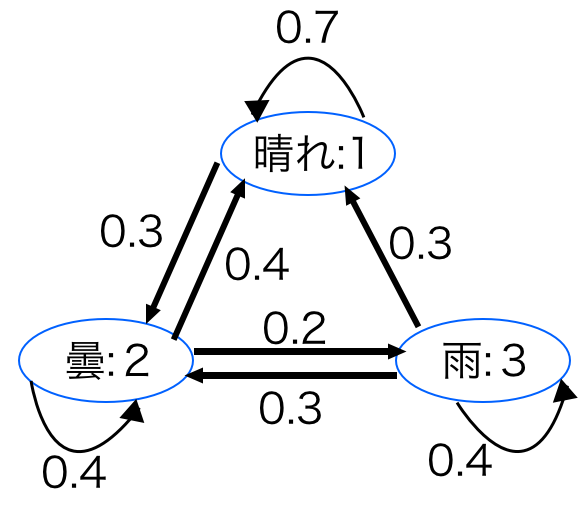
マルコフ性のもつ確率過程はマルコフ過程と呼ばれる。マルコフ過程で最も知られているのはマルコフ連鎖だが、他にも様々な過程があり、ブラウン運動もマルコフ性を有する。

次の性質はマルコフ性と定義される：

「現在状態が明らかなら、未来状態は過去履歴から独立して予測される」

確率過程 $X(t)$ が次の条件を満たすとき、この確率過程はマルコフ性を持つ：

\mathrm {Pr} {\big [}X(t h)=y\,|\,X(s)=x(s),\forall s\leq t{\big ]}=\mathrm {Pr} {\big [}X(t h)=y\,|\,X(t)=x(t){\big ]},\quad \forall h>0.

以下が成り立つマルコフ過程を「斉時的; time-homogeneous」であるという。

\mathrm {Pr} {\big [}X(t h)=y\,|\,X(t)=x{\big ]}=\mathrm {Pr} {\big [}X(h)=y\,|\,X(0)=x{\big ]},\quad \forall t,h>0,

そうでない場合は「非斉時的; time-inhomogeneous」であるという。斉時的マルコフ過程は一般に非斉時的過程よりも単純であり、マルコフ過程の中でも最も重要なクラスである。

実際にはマルコフ過程でないものを「現在」状態や「将来」状態の概念を拡張することでマルコフ過程的に表現することもある。例えば、X が非マルコフ過程であるとする。ここで、X における状態間の時間間隔を過程 Y の各状態とする。これを数式で表すと次のようになる。

Y(t)={\big \{}X(s):s\in [a(t),b(t)]\,{\big \}}.

Y がマルコフ性を持つ場合、それは X のマルコフ的表現となる。この場合 X を二階マルコフ過程（second-order Markov process）と呼ぶ。高階マルコフ過程も同様に定義される。

非マルコフ過程のマルコフ的表現の例として、移動平均を時系列に並べた移動平均線がある。