フールマン三角形

フールマン三角形（フールマンさんかくけい、英: Fuhrmann triangle）は、ヴィルヘルム・フールマン (1833–1904)にちなんで名付けられた特別な三角形である。

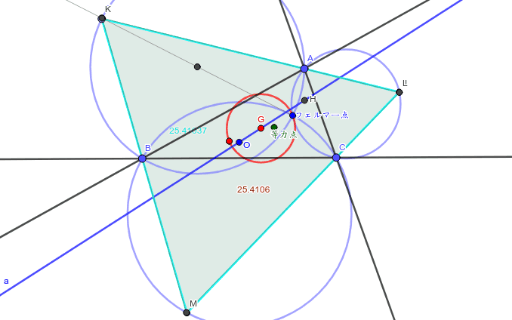
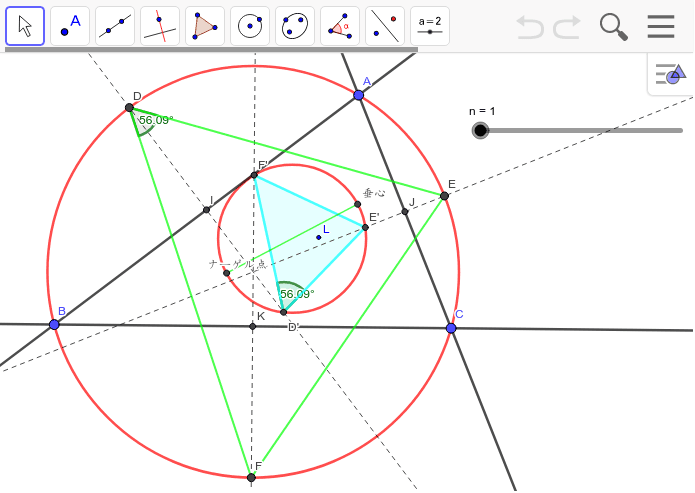
△ABCについて、その外接円の、それぞれA,B,Cを含まない円弧BC,CA,ABの中点をそれぞれM_a,M_b,M_cとする。これらの点を三角形の辺BC,CA,ABで鏡映した点M'_a,M'_b,M'_cが作る三角形をフールマン三角形という。

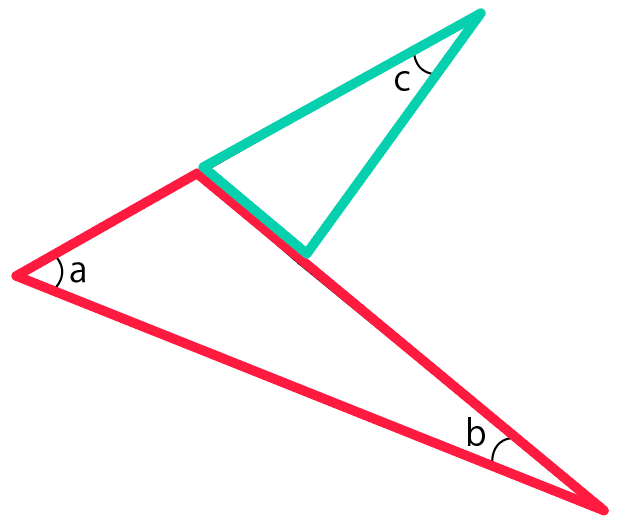
フールマン三角形の外接円は、フールマン円と呼ばれる。フールマン三角形は弧の中点が成す三角形と逆向きに相似、つまり△M_aM_bM_c~△M'_aM'_bM'_c である。フールマン三角形の面積について、以下の式が成り立つ 。

${\displaystyle |\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }|={\frac {s|OI|^{2}}{2R}}={\frac {s(R-2r)}{2}}}$

ここで、 Oは外心、Rは外接円の半径、Iは内心、sは半周長、rは内接円の半径である。右辺はオイラーの定理${\displaystyle |OI|^{2}=R(R-2r)}$による変形である。フールマン三角形の辺については以下の式が成り立つ。

${\displaystyle a^{\prime }=2{\sqrt {\frac {s(s-a)}{bc}}}|OI|={\sqrt {\frac {a(s-a)(R-2r)}{r}}}}$

${\displaystyle b^{\prime }=2{\sqrt {\frac {s(s-b)}{ac}}}|OI|={\sqrt {\frac {b(s-b)(R-2r)}{r}}}}$

${\displaystyle c^{\prime }=2{\sqrt {\frac {s(s-c)}{ab}}}|OI|={\sqrt {\frac {c(s-c)(R-2r)}{r}}}}$

ここで、a,b,cは各辺の長さである。

フールマン三角形と、基準三角形の対応は以下のとおりである。

一般化

△ABCと点Pについて、Pの擬調和三角形を△M_aM_bM_c、BC,CA,ABでM_a,M_b,M_cを鏡映した点をM'_a,M'_b,M'_cとする。△M'_aM'_bM'_cをPフールマン三角形（P-Fuhrmann triangle）という。Pの擬調和三角形とフールマン三角形は逆向きに相似である。Pフールマン三角形の外接円はPフールマン円、またはPヘギー円と呼ばれる。Pが内心のときは単にフールマン三角形、フールマン円である。

出典